프로그래머스 2019 윈터코딩 온라인 테스트를 보았다. (풀이)
첫 번째 문제에서 테스트케이스의 일부분이 실패하길래 디버깅하다가 1시간을 쓴 것 같다..
(0이 들어오진 않고, 로직은 맞았으나 형 변환을 하지 않아서 틀렸다.) - 19/11/16
많이 아쉬웠던 건 모든 문제에 대해서 접근 방법과 구현 방법이 떠올랐는데,
제대로 된 정답을 내지 못한 것이다.
대체로 요번 윈터코딩에서는 규칙성을 찾는 문제 위주로 나온 것 같다.
2번 문제는 정답이지만, 1번 부분점수 상태에서 디버깅 하다가 3번을 제대로 못풀고..
그래서 아쉬운 대로 내가 풀었던 방법을 적어놓고자 한다.
(현재 모든 문제 해결하였습니다.)
N x M 격자판에 양 꼭짓점으로 대각선을 하나 그었을 때,
직선에 걸치는 사각형을 전체 사각형의 개수에서 빼는 문제이다.
격자의 최소 단위는 1 x 1로 이루어져 있고, w와 h가 주어진다. (범위는 1억까지)
규칙을 찾다가, 정사각형일 때와 아닐 때를 생각해보았다.
정사각형인 N x N 형태이면, 대각선으로만 걸치므로 w * w - w를 하면 된다.
정사각형이 아닌 N x M 형태이면,
선에 걸치는 사각형들이 오른쪽 또는 아래를 걸쳐서 선을 타고 내려오는 모습이 된다.
(그림 참조)
3x3 사각형과 8x12 사각형
대각선이 아닌 오른쪽 또는 아래로만 거쳐서 선에 걸치는 사각형만 있으면 생각하기 쉽다.
그러나, 문제에서 주어진 예제 테스트케이스로 w=8, h=12를 생각해보면
중간마다 정사각형일 때 처럼, 대각선으로 걸치는 경우도 있다.
이 경우가 언제인지를 생각해보자.
그림에서 보면 정확히 2 x 3지점에서 대각선으로 걸치고 있다.
그리고 전체가 2 x 3인 사각형들을 4번 대각선으로 붙인 모습이다.
여기서 생각해볼 수 있는 건 이 2 x 3이 현재 전체 사각형들이 대각선으로 걸치는 최소 단위라는 것이다.
직선이므로, 내부에 존재하는 부분 직선도 기울기가 모두 같다.
따라서, 8/12 = 2/3이므로 주어지는 w, h를 모두 약분하면 최소 단위라고 볼 수 있다.
w와 h의 최대공약수를 구하면 4 = GCD(8, 12)이고
w와 h를 4로 나누면 2와 3이 된다. 이것이 총 4번 존재한다.
여기에서 식을 작성하기 전에 해야 할 하나의 작업이 남아있다.
바로 더 약분할 수 없는 상태일 때, 사각형의 개수를 구하는 작업이다.
2 x 3은 오른쪽 또는 아래로만 지나서 내려오므로 걸치는 사각형의 개수는 4개이다.
5 x 7도 오른쪽 또는 아래로만 지나서 내려오므로 걸치는 사각형의 개수는 11개이다.
따라서, 이를 식으로 표현하면 (w' + h' - 1)이 되며
이는 위의 최대공약수를 활용하면 (w / GCD(w, h) + h / GCD(w, h) - 1)이 된다.
원래의 w, h에 대한 식을 총정리하여
t = GCD(w, h)이라고 하면,
w * h - (w / t + h / t - 1) * t 라는 식이 완성된다.
[핵심 코드]
long long t = GCD(w, h);
return (long long)w * h - (w / t + h / t - 1) * t;
#2 종이 접기
종이를 정확히 반으로 접고 폈을 때, 접힌 부분을 체크하는 문제이다.
예를 들어 종이를 원래대로 쫙 폈을 때, 접힌 부분이 오목하다면 0 볼록하다면 1이다.
종이를 계속해서 접을수록 크기가 1/2이 되면서 접힌 부분도 2배로 늘어난다.
아래는 해결한 방법이다.
밑에서는 접힌 부분을 접선이라고 하자.
n은 접는 횟수로 기본값으로 n=1이면 0으로 생각한다.
n=2이면 0 0 1인데, n=1에서 접선인 부분을 제외한 또 다른 접선이 2배 생겨난다.
아직은 규칙을 정확히 모르겠으니, 시행 횟수를 늘려본다.
n = 1 0
n = 2 0 0 1
n = 3 0 0 1 0 0 1 1
n = 4 0 0 1 0 0 1 1 0 0 0 1 1 0 1 1
...
n = 1 0
n = 2 0 0 1
n = 3 0 0 1 0 0 1 1
n = 4 0 0 1 0 0 1 1 0 0 0 1 1 0 1 1
...
4번 접으니 규칙성이 보인다.
일단은, 문자열의 길이는 2^n - 1이다.
앞 부분을 보면 이전 문자열의 모습이 보이며, 정중앙에는 0이 들어간다.
그러면 남은 뒷부분의 길이는 n이 자명하다.
이제 뒷부분의 규칙만 찾으면 된다.
이전 문자열의 모습과 거의 비슷한데 무언가 다르다.
바로 중앙값의 변화다.
이전 문자열에서 중간에 있는 0을 1로 바꾸고 뒷부분에 이어 붙이면 규칙을 만족하게 된다.
[핵심 코드]
vector<int> sub = answer;
sub[sub.size() / 2] = 1; answer.push_back(0); for (int i = 0; i < sub.size(); ++i) answer.push_back(sub[i]);
#3 지형 이동
먼저 최대 크기가 300x300으로 완전 탐색(brute-force)으로 풀면 시간 초과가 발생한다.
문제를 해석해보면, 최단 경로가 아닌 어떤 경로로 가든지 최소 비용을 묻는다.
입출력 예제를 보면 알 수 있듯이, 어떤 칸에서 다른 칸으로 이동할 때 높이의 차가
주어진 높이(height) 이하이면 이동할 때 드는 비용이 없다.
또 높이의 차가 주어진 높이를 초과하면 비용이 든다.
즉, 여러 칸을 돌아서 가더라도 최소의 비용으로 연결할 수 있는 하나의 경로만 찾으면 된다.
여기까지 진행하고, 최소 스패닝 트리(minimum spanning tree)를 알고리즘을 사용하여 해결할 수 있다는 생각이 들었다.
그러면 대략적인 데이터의 크기를 계산해보자.
300x300이므로 최대 노드의 수는 V = 90,000
한 노드당 최대 간선의 개수는 4개이므로 E = 90,000 x 4 = 360,000
이정도면 해결하기에 충분한 시간이다.
(코딩테스트에서 평균적으로 1초에 1억 개 이상의 데이터를 다루는 것을 시간 초과의 기준으로 잡으면 편하다.
연산속도에 따라서 달라질 수 있으며, 시간제한을 더 넉넉하게 주는 경우도 있다.)
최소 스패닝 트리를 구성하는 알고리즘은 2가지가 있다.
크루스칼 알고리즘(Kruskal's algorithm)의 시간 복잡도는 O(ElogE)이고,
프림 알고리즘(Prim's algorithm)의 시간 복잡도는 O(ElogV)이다.
여기에서 간선의 개수가 많아서 프림 알고리즘으로 해결하기로 했다.
문제를 푸는 과정에서, 간선에 대한 정보는 없고 2차원 배열만 주어지기 때문에
인접한 원소들끼리는 간선이 될 수 있다고 생각하고 만들어 주어야 한다.
배열의 인덱스를 벗어나는 범위를 잘 처리해주고 모두 edge에 넣어준다.
이때, 인접한 원소의 크기의 차가 주어진 높이인 height 이하라면 가중치를 0을 넣고,
height 초과라면 abs(a - b)만큼 넣어준다.
이렇게 만들어진 edge를 통해 프림 알고리즘을 이용하면 답을 구할 수 있다.
[핵심 코드]
vector<pair<int, int>> edge[n * n + 1];
for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { if (i < n - 1) { int c = abs(land[i][j] - land[i + 1][j]); if (c <= height) c = 0; edge[i * n + j + 1].push_back({(i + 1) * n + j + 1, c}); } if (i > 0) { //... } if (j < n - 1) { //... } if (j > 0) { //... } } } int result = 0; priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> dist; bool visited[100001] = { false }; dist.push({1, 0}); for (int i = 1; i <= n * n; ++i) { int now = -1; int minDist = INT_MAX; while (!dist.empty()) { now = dist.top().first; if (!visited[now]) { minDist = dist.top().second; break; } dist.pop(); } result += minDist; visited[now] = true; for(auto &e : edge[now]) dist.push(e); }
return result;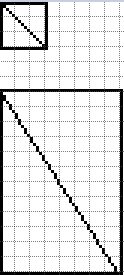
댓글
댓글 쓰기